Distributed ARIMA models for Ultra-long Time Series
Xiaoqian Wang
Beihang University
Joint work with Yanfei Kang, Rob J Hyndman and Feng Li
2020-10-26
Background
Ultra-long time series are increasingly accumulated in many cases.
- hourly electricity demands
- daily maximum temperatures
- streaming data generated in real-time
Forecasting these time series is challenging.
- time-consuming training process
- hardware requirements
- unrealistic assumption that the DGP remains invariant over a long time interval
Some attempts are made in the vast literature.
- discard the earliest observations
- allow the model itself to evolve over time
- apply a model-free prediction
- develop methods using the Spark’s MLlib library
P1: Ultra-long time series are becoming increasingly common. Examples include hourly electricity demands spanning several years, daily maximum temperatures recorded for hundreds of years, and streaming data
P2: It is challenging to deal with such long time series. We identify three significant challenges, including:
- time-consuming training process, especially parameters optimization
- hardware requirements
- unrealistic assumption that the DGP remains invariant over a long time interval
P3: Forecasters have made some attempts to address these limitations.
- a straightforward approach is to discard the earliest observationsonly, it only works well for forecasting a few future values
- allow the model itself to evolve over time, such as ARIMA and ETS
- apply a model-free prediction assuming that the series changes slowly and smoothly with time (2,3) require considerable computational time in model fitting and parameter optimization, making them less practically useful in modern enterprises
- develop methods using the Spark’s MLlib library. However, the platform does not support the multi-step prediction, convert the multi-step time series prediction problem into H sub-problems, H is the forecast horizon We argue that there is a preferable way to resolve the challenges
Electricity load data
The Global Energy Forecasting Competition 2017 (GEFCom2017)
Hourly electricity load data of zones spanning New England
\(8\) bottom zones & \(2\) aggregated zones
without considering the hierarchical configuration
Ranging from March 1, 2003 to April 30, 2017 ( \(124,171\) time points)
training periods
March 1, 2003 - December 31, 2016test periods
January 1, 2017 - April 30, 2017 ( \(h=2,879\) )
- We use electricity load data of the Global Energy Forecasting Competition as examples.
- The dataset contains 10 hourly electricity demand series of New England. There are 8 bottom and 2 aggregated zones. But we don’t consider the hierarchical configuration here.
- Each series spans 14 years. We aim to forecast observations of the next 4 months.
Electricity load data
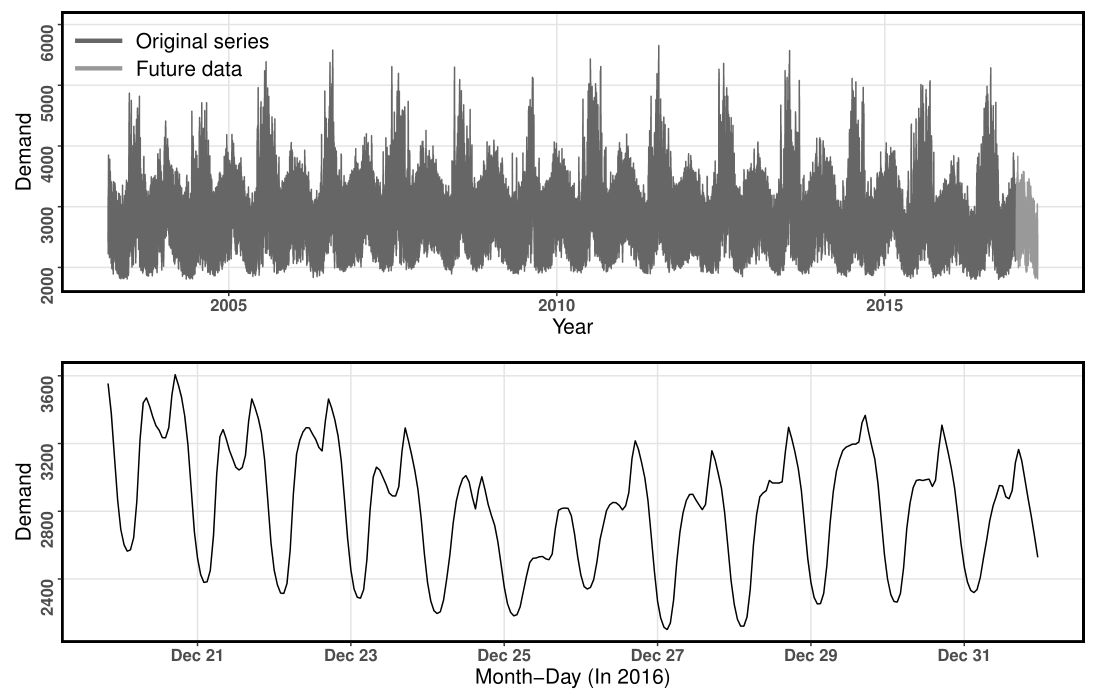
The electricity demand example for NEMASSBOST zone from GEFCom2017 dataset.
Here is an example series. The top panel shows the whole series, the bottom panel shows a clip of half a month.
- The yearly and hourly seasonal patterns can be observed.
- The DGP of the series has changed over the 14 years, although the change is not obvious due to the large electricity demand values.
Distributed forecasting
Zhu, Li & Wang (2019) tackle regression problems on distributed systems by developing a distributed least squares approximation (DLSA) method.
Local estimators are computed by worker nodes in a parallel manner.
Local estimators are delivered to the master node to approximate global estimators by taking a weighted average.
In this work, we want to find a better way to resolve all challenges associated with forecasting ultra-long time series. (...) Inspired by this, we aim to extend the DLSA method to solve the time series modeling problem.
Distributed forecasting
Parameter estimation problem
For an ultra-long time series \(\left\{y_{t}; t=1, 2, \ldots , T \right\}\). Define \(\mathcal{S}=\{1, 2, \cdots, T\}\) to be the timestamp sequence.
The parameter estimation problem can be formulated as $$ f\left( \theta ,\Sigma | y_t, t \in \mathcal{S} \right). $$
Distributed forecasting
Parameter estimation problem
For an ultra-long time series \(\left\{y_{t}; t=1, 2, \ldots , T \right\}\). Define \(\mathcal{S}=\{1, 2, \cdots, T\}\) to be the timestamp sequence.
The parameter estimation problem can be formulated as $$ f\left( \theta ,\Sigma | y_t, t \in \mathcal{S} \right). $$
Suppose the whole time series is split into \(K\) subseries with contiguous time intervals, that is \(\mathcal{S}=\cup_{k=1}^{K} \mathcal{S}_{k}\).
The parameter estimation problem is transformed into \(K\) sub-problems and one combination problem as follows: $$ f\left( \theta ,\Sigma | y_t, t \in \mathcal{S} \right) = g\big( f_1\left( \theta_1 ,\Sigma_1 | y_t, t \in \mathcal{S}_1 \right), \ldots, f_K\left( \theta_K ,\Sigma_K | y_t, t \in \mathcal{S}_K \right) \big). $$
We identify the parameter estimation problem as this formula ~.
Distributed forecasting
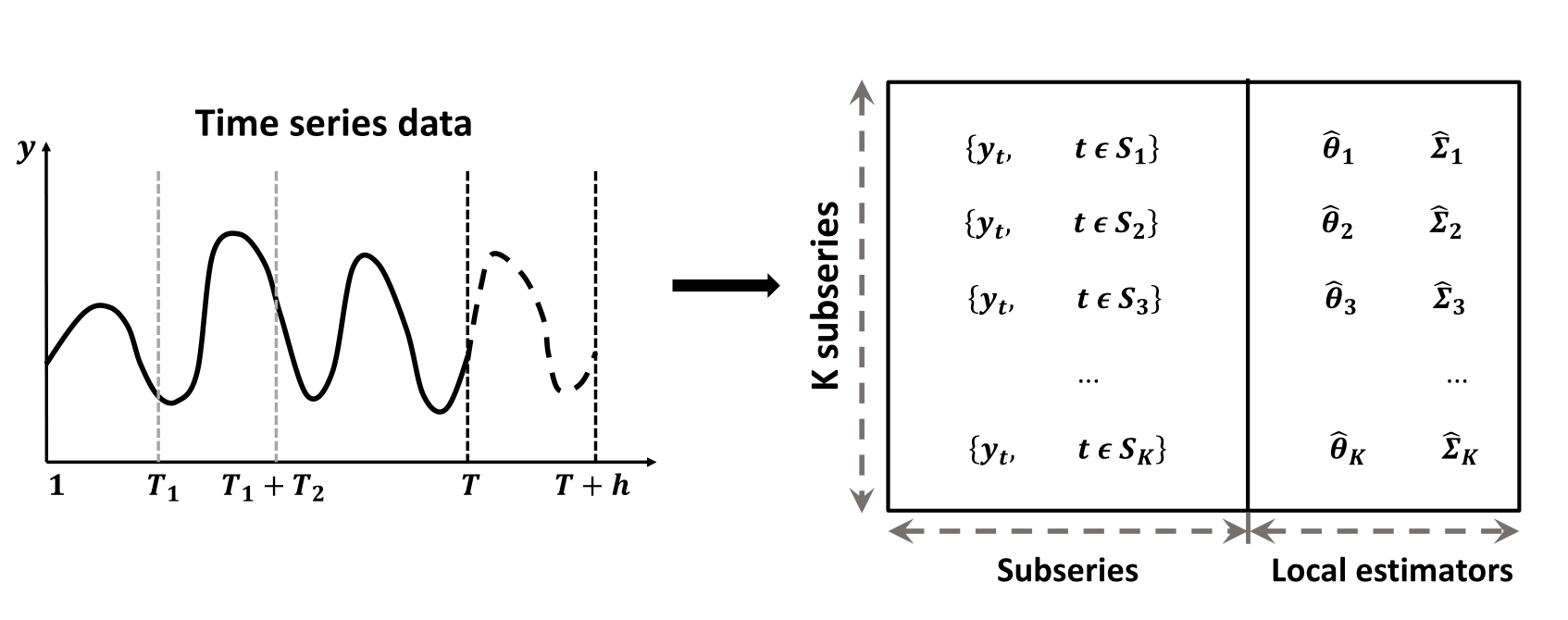
Illustration of forecasting problem and time series split.
Distributed forecasting
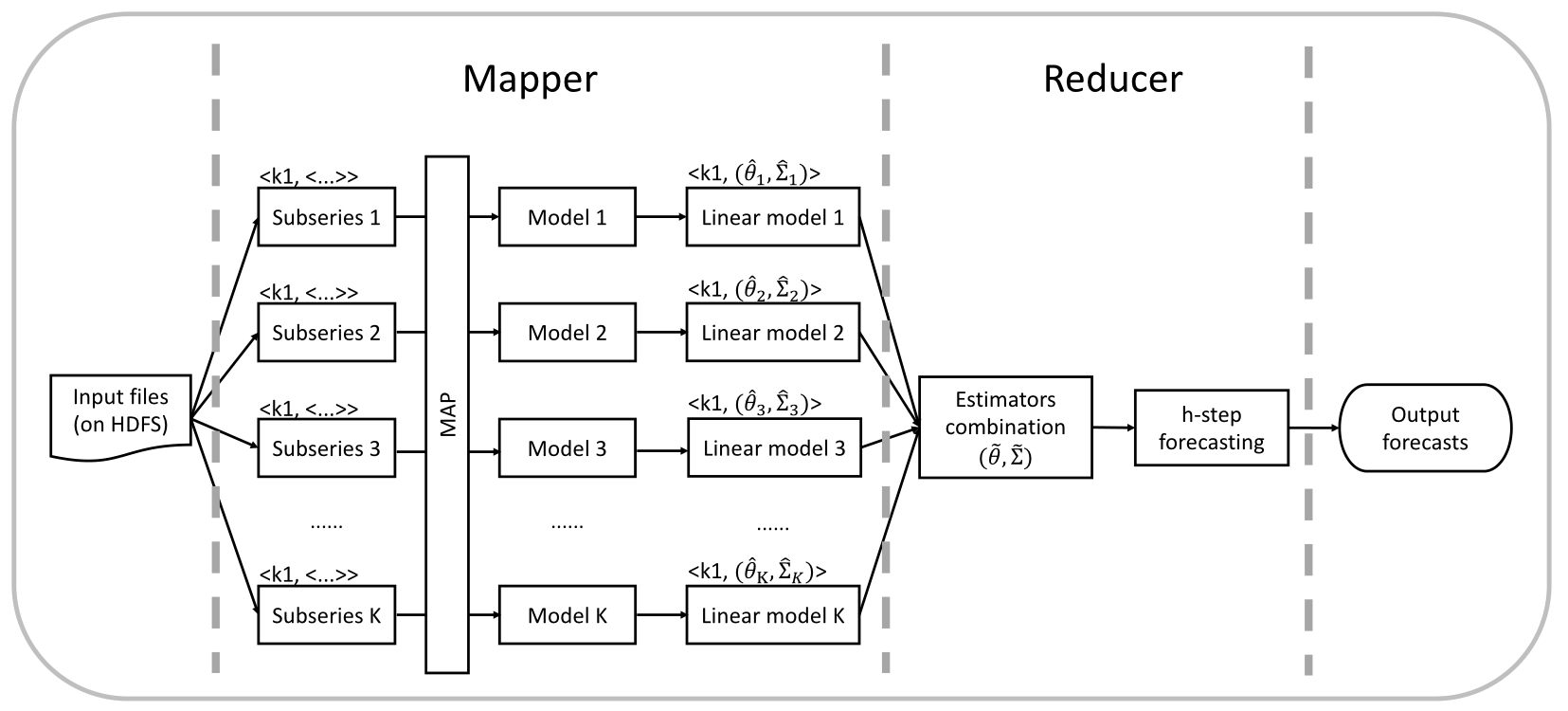
The proposed framework for time series forecasting on a distributed system.
- Step 1: Preprocessing.
- Step 2: Modeling.
- Step 3: Linear transformation.
- Step 4: Estimator combination.
- Step 5: Forecasting.
Why focus on ARIMA models
Advantages
The most widely used statistical time series approachs.
ARIMA models can handle non-stationary series via differencing and seasonal patterns
ARIMA models frequently serve as benchmark methods for model combination because of their excellent performance in forecasting.
ARIMA models can be converted into AR representations (linear form).
Hyndman & Khandakar (2008) developed the automatic time series forecasting with ARIMA models to easily implement the order selection process.
Limitations
- The likelihood function of such time series model could hardly scale up.
We suggest that our approach is general and can be applied to other types of forecasting models. But, in the work, we focus on ARIMA models due to their good properties.
- The linear form makes it easy for the estimators combination Limitations:
- Due to the nature of time dependence, the likelihood function of such time series model could hardly scale up, making it infeasible for massive time series forecasting.
Automatic ARIMA modeling
The procedure of an automatic ARIMA forecasting framework, taking the auto.arima() algorithm as an example.
The automatic ARIMA modeling mainly consists of 3 steps... Where the order selection and model refit process are time-consuming for ultra-long time series. The time spend in forecasting one electricity demand series ranges from 20 minutes to 2 hours. So, it is necessary to develop a new approach to make ARIMA models work well for ultra-long series.
AR representation
- A seasonal ARIMA model is generally defined as \begin{align} \left(1-\sum_{i=1}^{p}\phi_{i} B^{i}\right) \left(1-\sum_{i=1}^{P}\Phi_{i} B^{im}\right)(1-B)^{d}\left(1-B^{m}\right)^{D} \left(y_{t} - \mu_0 - \mu_1 t \right) \nonumber \\ =\left(1+\sum_{i=1}^{q}\theta_{i} B^{i}\right)\left(1+\sum_{i=1}^{Q}\Theta_{i} B^{im}\right) \varepsilon_{t}. \end{align}
AR representation
A seasonal ARIMA model is generally defined as \begin{align} \left(1-\sum_{i=1}^{p}\phi_{i} B^{i}\right) \left(1-\sum_{i=1}^{P}\Phi_{i} B^{im}\right)(1-B)^{d}\left(1-B^{m}\right)^{D} \left(y_{t} - \mu_0 - \mu_1 t \right) \nonumber \\ =\left(1+\sum_{i=1}^{q}\theta_{i} B^{i}\right)\left(1+\sum_{i=1}^{Q}\Theta_{i} B^{im}\right) \varepsilon_{t}. \end{align}
Let the term \(y_{t} - \mu_0 - \mu_1 t\) be denoted as \(x_t\).
By utilizing the polynomial multiplication, the seasonal ARIMA model is converted into a non-seasonal ARMA( \(u,v\) ) model (possibly non-stationary) \begin{align} \left(1-\sum_{i=1}^{u}\phi_{i}^{\prime} B^{i}\right) x_{t}=\left(1+\sum_{i=1}^{v}\theta_{i}^{\prime} B^{i}\right) \varepsilon_{t}. \end{align}
AR representation
The AR representation of the ARMA( \(u,v\) ) can be obtained by long division of AR and MA polynomials.
Given two polynomials \(\phi^{\prime}(B) = \left(1-\sum_{i=1}^{u}\phi_{i}^{\prime} B^{i}\right)\) and \(\theta^{\prime}(B) = \left(1+\sum_{i=1}^{v}\theta_{i}^{\prime} B^{i}\right)\), we have \begin{equation} \pi (B) x_t = \frac{\phi^{\prime}(B)}{\theta^{\prime}(B)} x_t = \varepsilon_{t}, \end{equation} where \(\pi (B) = \left(1-\sum_{i=1}^{\infty}\pi_{i} B^{i}\right)\).
AR representation
The AR representation of the ARMA( \(u,v\) ) can be obtained by long division of AR and MA polynomials.
Given two polynomials \(\phi^{\prime}(B) = \left(1-\sum_{i=1}^{u}\phi_{i}^{\prime} B^{i}\right)\) and \(\theta^{\prime}(B) = \left(1+\sum_{i=1}^{v}\theta_{i}^{\prime} B^{i}\right)\), we have \begin{equation} \pi (B) x_t = \frac{\phi^{\prime}(B)}{\theta^{\prime}(B)} x_t = \varepsilon_{t}, \end{equation} where \(\pi (B) = \left(1-\sum_{i=1}^{\infty}\pi_{i} B^{i}\right)\).
- The linear representation of the original seasonal ARIMA model can be given by \begin{equation} y_t = \beta_0 + \beta_1 t + \sum_{i=1}^{\infty}\pi_{i}y_{t-i} + \varepsilon_{t}, \end{equation} where \begin{equation} \beta_0 = \mu_0 \left( 1- \sum_{i=1}^{\infty}\pi_{i} \right) + \mu_1 \sum_{i=1}^{\infty}i\pi_{i} \qquad \text{and}\qquad \beta_1 = \mu_1 \left( 1- \sum_{i=1}^{\infty}\pi_{i} \right). \end{equation}
For a general seasonal ARIMA models, by using multiplication and long division of polynomials, we can obtain the final converted linear representation in this form. In this way, all ARIMA models fitted for subseries can be converted into this linear form.
Estimators combination
Some excellent statistical properties of the global estimator obtained by DLSA has been proved (Zhu, Li & Wang, 2019).
We extend the DLSA method to solve time series modeling problem.
Define \(\mathcal{L}(\theta; y_t)\) to be a second order differentiable loss function, we have \begin{align} \label{eq:loss} \mathcal{L}(\theta) &=\frac{1}{T} \sum_{k=1}^{K} \sum_{t \in \mathcal{S}_{k}} \mathcal{L}\left(\theta ; y_{t}\right) \nonumber \\ &=\frac{1}{T} \sum_{k=1}^{K} \sum_{t \in \mathcal{S}_{k}}\left\{\mathcal{L}\left(\theta ; y_{t}\right)-\mathcal{L}\left(\hat{\theta}_{k} ; y_{t}\right)\right\}+c_{1} \nonumber \\ & \approx \frac{1}{T} \sum_{k=1}^{K} \sum_{t \in \mathcal{S}_{k}}\left(\theta-\widehat{\theta}_{k}\right)^{\top} \ddot{\mathcal{L}}\left(\hat{\theta}_{k} ; y_{t}\right)\left(\theta-\hat{\theta}_{k}\right)+c_{2} \nonumber \\ &\approx \sum_{k=1}^{K} \left(\theta-\hat{\theta}_{k}\right)^{\top} \left(\frac{T_k}{T} \widehat{\Sigma}_{k}^{-1}\right) \left(\theta-\hat{\theta}_{k}\right)+c_{2}. \end{align}
- The next stage entails solving the problem of combining the local
- Taylor’s theorem & the relationship between the Hessian and covariance matrix for Gaussian random variables
- This leads to a weighted least squares form
Estimators combination
The global estimator calculated by minimizing the weighted least squares takes the following form \begin{align} \tilde{\theta} &= \left(\sum_{k=1}^{K}\frac{T_k}{T}\widehat{\Sigma}_{k}^{-1}\right)^{-1}\left(\sum_{k=1}^{K}\frac{T_k}{T}\widehat{\Sigma}_{k}^{-1}\hat{\theta}_{k}\right), \\ \tilde{\Sigma} &= \left(\sum_{k=1}^{K}\frac{T_k}{T}\widehat{\Sigma}_{k}^{-1}\right)^{-1}. \end{align}
\(\widehat{\Sigma}_{k}\) is not known and has to be estimated.
We approximate a GLS estimator by an OLS estimator (e.g., Hyndman et al., 2011) while still obtaining consistency.
We consider approximating \(\widehat{\Sigma}_{k}\) by \(\hat{\sigma}_{k}^{2}I\) for each subseries.
The global estimator and its covariance matrix can be obtained. The covariance matrix of subseries is not known, so we estimate it by sigma2I.
Point forecasts
The \(h\)-step-ahead forecast can be calculated as \begin{equation} \hat{y}_{T+h | T}=\tilde{\beta}_{0}+\tilde{\beta}_{1}(T+h)+\left\{\begin{array}{ll}\sum_{i=1}^{p} \tilde{\pi}_{i} y_{T+1-i}, & h=1 \\ \sum_{i=1}^{h-1} \tilde{\pi}_{i} \hat{y}_{T+h-i | T}+\sum_{i=h}^{p} \tilde{\pi}_{i} y_{T+h-i}, & 1<h<p. \\ \sum_{i=1}^{p} \tilde{\pi}_{i} \hat{y}_{T+h-i | T}, & h \geq p\end{array}\right. \end{equation}
Then, the point forecasts and prediction intervals can be obtained.
Prediction intervals
In the global model, the standard error of \(h\)-step ahead forecast is formally expressed as \begin{equation} \tilde{\sigma}_{h}^{2} = \left\{ \begin{array}{ll} \tilde{\sigma}^{2}, & h = 1 \\ \tilde{\sigma}^{2}\left( 1 + \sum_{i=1}^{h-1}\tilde{\theta}_{i}^{2} \right), & h > 1 \\ \end{array}, \right. \end{equation} where \(\tilde{\sigma}^{2}= \operatorname{tr}(\tilde{\Sigma})/p\).
The central \((1-\alpha) \times 100 \%\) prediction interval of \(h\)-step ahead forecast can be defined as \begin{equation} \hat{y}_{T+h|T} \pm \Phi^{-1}\left(1-\alpha/2\right)\tilde{\sigma}_{h}. \end{equation}
Experimental setup
Number of subseries: \(150\)
- the length of each subseries about \(800\)
- the hourly time series in M4 ranges from \(700\) to \(900\)
- the time consumed by automatic ARIMA modeling process is within 5 minutes
AR order: \(2000\)
The experiments are carried out on a Spark-on-YARN cluster
- one master node and two worker nodes
- Each node contains 32 logical cores, 64 GB RAM and two 80GB SSD local hard drives
Distributed forecasting results
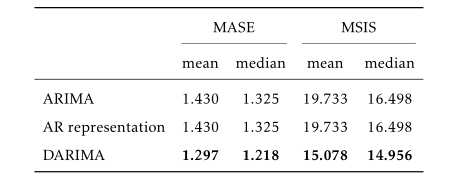
Benchmarking the performance of DARIMA against ARIMA model and its AR representation.
The rationality of setting the AR order to \(2000\).
DARIMA always outperforms the benchmark method regardless of point forecasts or prediction intervals.
Distributed forecasting results
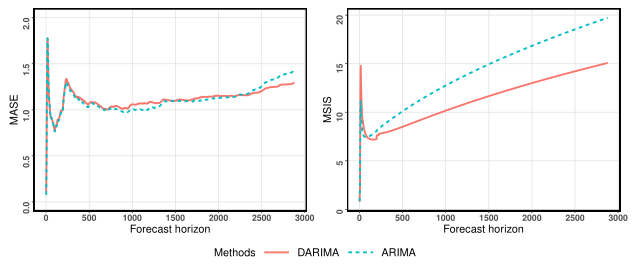
Benchmarking the performance of DARIMA against ARIMA for various forecast horizons.
If long-term observations are considered, DARIMA is preferable, especially for interval forecasting.
The achieved performance improvements of DARIMA become more pronounced as the forecast horizon increases.
Distributed forecasting results
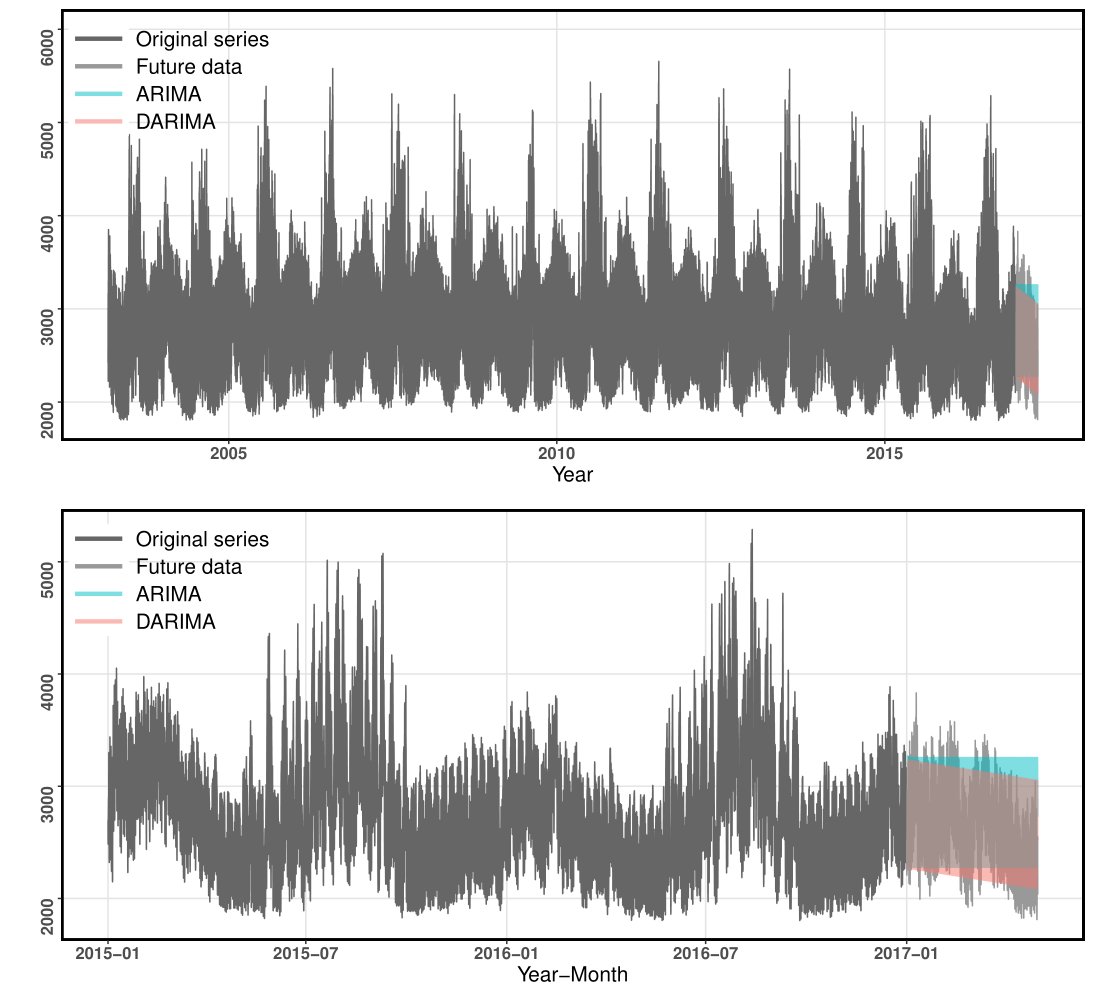
Distributed forecasting results
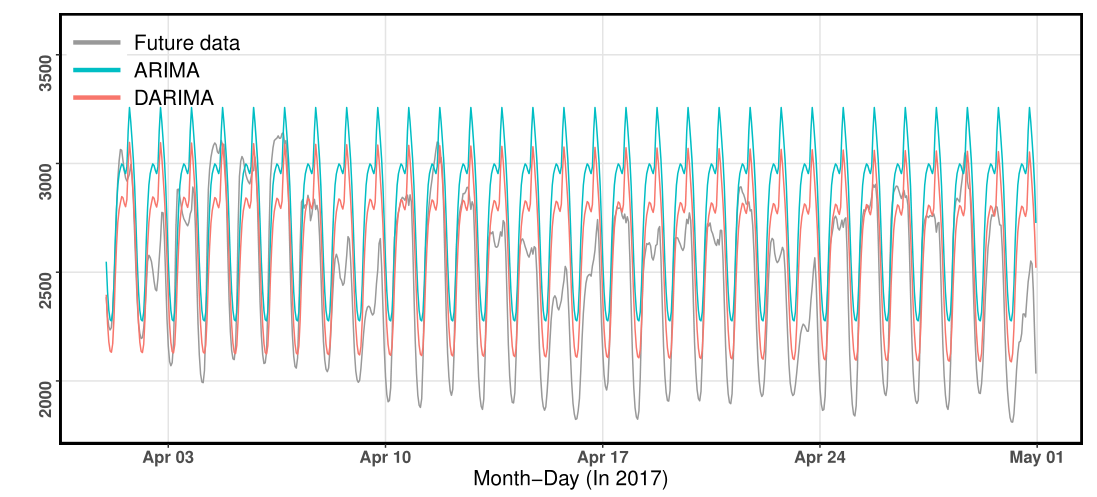
Our approach has captured the decreasing yearly seasonal trend.
Both DARIMA and ARIMA have captured the hourly seasonality, while DARIMA results in forecasts closer to the true future values than ARIMA.
Distributed forecasting results
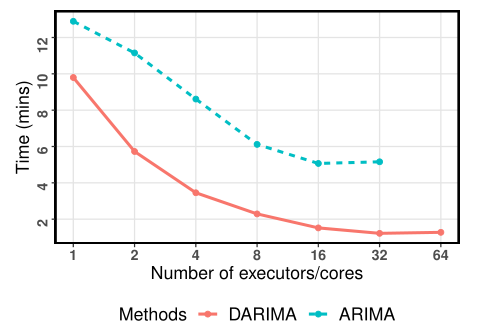
- MSIS results across different confidence levels
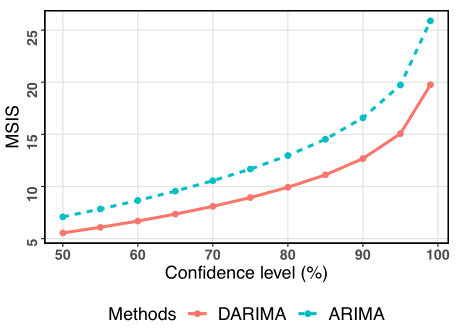
- Execution time
Sensitivity analysis
Number of split subseries
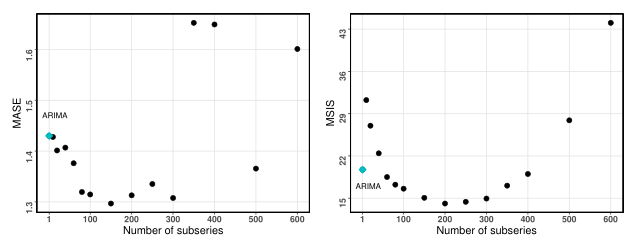
Relationship between the forecasting performance of DARIMA models and the number of subseries.
- The number of subseries should be controlled within a reasonable range, with too few or too many subseries causing poor forecasting performance.
- In particular, the relationship between the number of subseries and the MISS values shows as a concave line.
Sensitivity analysis
Maximum values of model orders
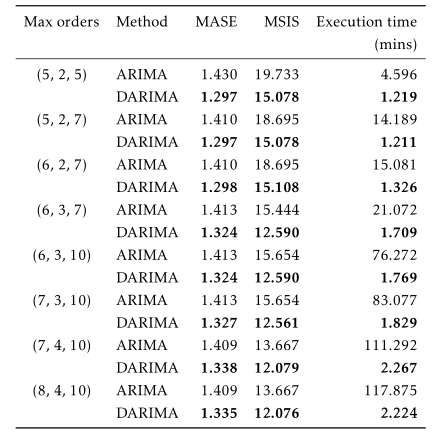
forecasting performance
computational efficiency
broader range of candidate models
Summary
A distributed time series forecasting framework using the industry-standard MapReduce framework.
The local estimators trained on each subseries are combined using weighted least squares to minimize a global loss function.
Our framework
works better than competing methods for long-term forecasting.
achieves improved computational efficiency in optimizing the model parameters.
allows that the DGP of each subseries could vary.
can be viewed as a model combination approach.
Thanks!
Spark implementation: https://github.com/xqnwang/darima
Website: https://xqnwang.rbind.io